Penghitungan yang lebih mudah
Logaritma memindahkan fokus penghitungan dari bilangan normal ke
pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa
jenis penghitungan menjadi lebih mudah menggunakan logaritma::
| Penghitungan dengan angka |
Penghitungan dengan eksponen |
Identitas Logaritma |
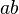 |
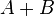 |
 |
 |
 |
 |
 |
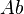 |
 |
![\!\, \sqrt[b]{a}](http://upload.wikimedia.org/wikipedia/id/math/5/3/4/53461f66c006c3895b99f26c37688dea.png) |
 |
![\!\, \log(\sqrt[b]{a}) = \frac{\log(a)}{b}](http://upload.wikimedia.org/wikipedia/id/math/f/6/7/f678f8a14d7cc1e5fb5f20825525e009.png) |
Sifat-sifat di atas membuat penghitungan dengan eksponen menjadi
lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum
tersedianya
kalkulator sebagai hasil perkembangan teknologi modern.
Untuk mengkali dua angka, yang diperlukan adalah melihat logaritma
masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog
jumlah tersebut dalam tabel. Untuk mengitung pangkat atau akar dari
sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel,
lalu hanya mengkali atau membagi dengan
radix pangkat atau akar tersebut.
Kalkulus
Turunan fungsi logaritma adalah
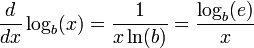
dimana ln adalah logaritma natural, yaitu logaritma yang berbasis
e. Jika
b =
e, maka rumus di atas dapat disederhanakan menjadi
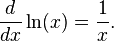
Integral fungsi logaritma adalah
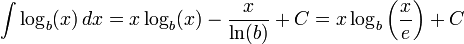
Integral logaritma berbasis e adalah

Sebagai contoh carilah turunan
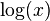
Penghitungan nilai logaritma
Nilai logaritma dengan basis b dapat dihitung dengan rumus dibawah ini.

Sedangkan untuk logaritma berbasis e dan berbasis 2, terdapat
prosedur-prosedur yang umum, yang hanya menggunakan penjumlahan,
pengurangan, pengkalian, dan pembagian.
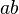
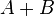





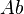

![\!\, \sqrt[b]{a}](http://upload.wikimedia.org/wikipedia/id/math/5/3/4/53461f66c006c3895b99f26c37688dea.png)

![\!\, \log(\sqrt[b]{a}) = \frac{\log(a)}{b}](http://upload.wikimedia.org/wikipedia/id/math/f/6/7/f678f8a14d7cc1e5fb5f20825525e009.png)
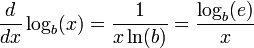
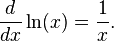
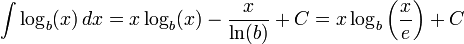

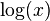

Tidak ada komentar:
Posting Komentar